第五章 自相關 Autocorrelation
在前一章我將白噪音的性質視為「不相關」,因為它的每個值都各自獨立,而把布朗噪音的性質視為「相關」,因為它的每個值都與依據前值。在這章我會更精確定義這些詞,並介紹「自相關函數 autocorrelation function」,這是訊號分析很有用的工具。在開始自相關之前,我們從相關開始。
這章的程式碼在 chap05.ipynb,所在位置請見 0.2 節。你也可以參見 http://tinyurl.com/thinkdsp05
5.1 相關 | Correlation
一般來說,變數之間的相關指的是,如果你知道其中一個值,你就有了一些其他值的線索,可以幫助你知道其他的值。有幾個方法可以量化這個相關性質,但是最常用的是「皮爾遜積矩相關係數 Pearson product-moment correlation coefficient」。常用的符號是 ρ。對兩個變數,x 與 y,每個變數有 N 個值:與 是 x 與 y 的平均值, 與 是它們的標準差。
皮爾遜相關總是在 -1 與 +1 之間(也包含-1 與 +1),如果 ρ 是正的,我們說這是正相關,意思是如果一個變數值是高的,那另一個也傾向是高的。如果 ρ 是負的,我們說這是負相關,所以當一個變數值是高的,那另一個就傾向是低的。
ρ 的數字表示相關的強度。如果 ρ 是 -1 或是 1,那變數是代表完全相關,表示如果你知道一個,就能完全預測另一個。如果 ρ 接近 0,相關大概很弱。所以如果你知道一個,你對其他的值還是無法知道。
我說大概很弱,因為也有可能是有非線性的關係,非線性關係不能被這個相關係數所捕捉到。非線性關係在統計上通常很重要,但是在訊號處理沒這麼重要,所以這裡不多談。
python 提供幾個方法計算相關,np.corrcoef 可以為任意數目的變數計算相關矩陣,它由每個變數兩兩之間的相關係數所組成。

圖5.1:兩個正弦波,相差 1 個弧度的相位。它們的相關係數是 0.54
我會從兩個變數的例子開始。首先我定義一個函數,會依相位差產生正弦波。
def make_wave(offset):
signal = thinkdsp.SinSignal(freq=440, offset=offset)
wave = signal.make_wave(duration=0.5, framerate=10000)
return wave
wave1 = make_wave(offset=0)
wave2 = make_wave(offset=1)
>>> corr_matrix = np.corrcoef(wave1.ys, wave2.ys, ddof=0)
[[ 1. 0.54]
[ 0.54 1. ]]
產生的結果是相關矩陣,第一個元素是 wave1 與自己的相關,所以永遠為 1。同樣的,最後一個元素是 wave2 與自己的相關。

圖5.2:兩個正弦波的相關,正是兩者之間相位差的函數。結果是一個餘弦函數。
非對角線元素包含我們有興趣的值,wave1 與 wave2 的相關。0.54 這個值表示相關的強度約是中等。
當相位差增加,相關就變小,直到波相差 180 度,此時相關為 -1。當它增加到相位差 360 度,此時相差正好一個完整週期,相關是 1。
圖5.2 顯示正弦波的相關與相位差的關係,它的曲線看起來應該很熟悉,是個餘弦曲線。
thinkdsp 提供一個簡單的介面來計算兩個波的相關:
>>> wave1.corr(wave2)
0.54
5.2 序列相關 | Serial correlation
訊號往往代表了隨著時間的數值的量測。例如,聲音訊號代表對電壓(或電流)的量測,它對應到我們認知的聲音是空氣壓力的變化。像這樣的量測總是會有序列相關存在於前後兩個元素之間。要計算序列相關,我們可以平移一個訊號,然後再計算平移過的與原來的訊號之間的相關。
def serial_corr(wave, lag=1):
n = len(wave)
y1 = wave.ys[lag:]
y2 = wave.ys[:n-lag]
corr = np.corrcoef(y1, y2, ddof=0)[0, 1]
return corr
我們可以用前一章的噪音訊號來測試這個函式。我們依據其產生的方式(而不是名字)預期 UU noise 是個不相關噪音,現在我們來看看:
signal = thinkdsp.UncorrelatedGaussianNoise()
wave = signal.make_wave(duration=0.5, framerate=11025)
serial_corr(wave)
當我執行這個範例,我得到 0.006,這代表是非常小的序列相關。你也許會得到不同的值,但一定都是相對小的值。
在一個布朗噪音訊號裡,每個值都是前值的總和再加個隨機步進值,所以我們預期它是非常強的序列相關的訊號:
signal = thinkdsp.BrownianNoise()
wave = signal.make_wave(duration=0.5, framerate=11025)
serial_corr(wave)
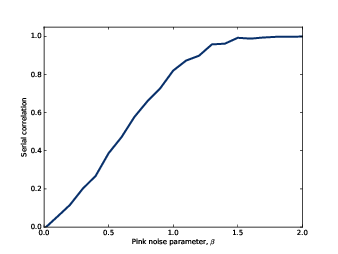
圖5.3:pink noise 的 beta 與序列相關的值的關係圖
因為 pink noise 是介在 UU noise 與布朗噪音之間,我們會猜測它的序列相關的值應該介在中間:
signal = thinkdsp.PinkNoise(beta=1)
wave = signal.make_wave(duration=0.5, framerate=11025)
serial_corr(wave)
5.3 自相關 | Autocorrelation
在前一節中,我們計算每個值與下個值之間的相關,所以我們將序列中的元素平移一格,也就是延遲一格。實際上,我們可以計算不同延遲(lag)的相關值。
圖5.4:pink noise 的自相關函數值。
你可以想像,serial_corr 是個函數,對應每個延遲(lag)到相關數,我們就可以用迴圈將延遲的值一個個用函數評估出相關數:
def autocorr(wave):
lags = range(len(wave.ys)//2)
corrs = [serial_corr(wave,lag) for lag in lags]
return lags, corrs圖5.4 顯示 pink noise 的自相關函數,裡面有三個不同值的 。對於低值的 來說,這訊號比較少相關,所以自相關函數就下降很快。對於大一點的值,序列相關就比較強一點,下降就慢一點。=1.7 就算長延遲其序列相關也很強。這現像叫 long-range dependence (長範圍相依),因為它指出每個值都與之前的很多值有依賴。
5.4 週期訊號的自相關 | Autocorrelation of periodic signals
pink noise 的自相關有著有趣的數學性質,但可利用的比較少。週期函數的自相關則比較多用途。
圖5.5:聲音唧頻的 pectrogram
舉例來說,我從 freesound.org 下載某個人唱歌的聲音,在本書的(repository)公開庫也包含這個檔案
28042__bcjordan__voicedownbew.wav。也可以用 jupyter notebook 開啟 chap05.ipynb 來播放它。
圖5.5 顯示這個波的 spectrogram,基頻與一些諧頻非常乾淨。這唧頻約在 500Hz 開始,約在 300 Hz 下降,大概接近 C5 到 E4 之間。
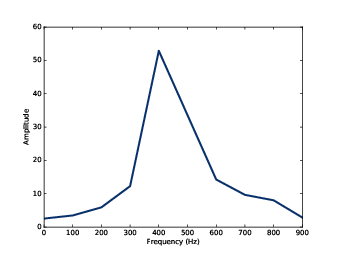
圖5.6:一個聲音唧頻的頻譜
要估計某時間點的音高,我們可以用頻譜,但它不是很好用。我們來看看為什麼不好用。我截出一段聲音,畫出它的頻譜:
duration = 0.01
segment = wave.segment(start=0.2, duration=duration)
spectrum = segment.make_spectrum()
spectrum.plot(high=1000)
我們可以拿更長的聲音段,以得到更好的頻率解析度,但因為音高會隨時間改變,我們也會得到 motion blur,也就是波峰會在啟始音高與結尾音高約為散開,如同我們在 3.3節看到的一樣。
我們可以用自相關(autocorrleation)做更準確的估計音高。如果一個訊號是週期的,我們預期當延遲等同週期時,自相關會很尖銳。

圖5.7:從一個唧頻取兩音段,兩個相差 0.0023 秒。
要解釋為什麼,我會從同樣的聲音畫兩個音段。
def plot_shifted(wave, offset=0.001, start=0.2):
thinkplot.preplot(2)
segment1 = wave.segment(start=start, duration=0.01)
segment1.plot(linewidth=2, alpha=0.8)
segment2 = wave.segment(start=start-offset, duration=0.01)
segment2.shift(offset)
segment2.plot(linewidth=2, alpha=0.4)
corr = segment1.corr(segment2)
text = r'$\rho =$ %.2g' % corr
thinkplot.text(segment1.start+0.0005, -0.8, text)
thinkplot.config(xlabel='Time (s)')
圖5.8:從唧率取的音段的自相關函數
在這個例子裡,我用試誤法估計週期。要自動化這個過程,我們可以使用自相關函數。
lags, corrs = autocorr(segment)
thinkplot.plot(lags, corrs)
period = lag / segment.framerate
frequency = 1 / period
5.5 相關視為點積 | Correlation as dot product
本章一開始,我定義了 相關係數 Pearson’s correlation cofficient:接下來使用 定義序列相關與自相關。這是與統計的詞彙統一。但在訊號處理的領域裡,定義有些不一樣。
在訊號處理中,我們常處理的是 unbiased signals 也就是平均值為零的訊號、normalized signals 也就是標準差為 1 的訊號。在這個例子裡, 可以簡化成:
通常這可以再簡化:
這樣定義的相關不是標準化的,所以它的值不會落在 -1 與 1 之間。但它有其他好用的性質。
如果你把 x 與 y 想成向量,你會發現這個方程式相同於點積 。請參閱 http://en.wikipedia.org/wiki/Dot_product
點積暗示訊號也有角度,如果它們也正規化後,將標準差整成 1 之後,
是兩個向量的角度。這也解釋為什麼圖5.2 是一個 cosine 曲線
5.6 使用 NumPy | Using NumPy
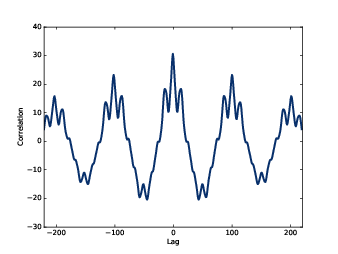
圖5.9:用 np.correlate 計算自相關函數
NumPy 提供一個函式,correlate,這計算兩個函數或一個函數的自相關函數的相關。我們可以用它來計算前一節的音樂的自相關:
corrs2 = np.correlate(segment.ys, segment.ys, mode='same')圖5.9 顯示了結果。它會對稱是因為兩個訊號是同一個,所以負的 lag 作用與正的 lag 作用一樣。為了要與 autocorr 做比較,我們可以選擇後半段:
N = len(corrs2)
half = corrs2[N//2:]我們可以用長度來除以修正:
lengths = range(N, N//2, -1)
half /= lengthshalf /= half[0]比較重要的是,現在我們知道什麼是自相關,如何使用它來計算一個訊號的基礎週期,以及計算它的兩種方式。
5.7 練習
Solutions to these exercises are in chap05soln.ipynb.Exercise 1 The Jupyter notebook for this chapter, chap05.ipynb, includes an interaction that lets you compute autocorrelations for different lags. Use this interaction to estimate the pitch of the vocal chirp for a few different start times.
Exercise 2 The example code in chap05.ipynb shows how to use autocorrelation to estimate the fundamental frequency of a periodic signal. Encapsulate this code in a function called estimate_fundamental, and use it to track the pitch of a recorded sound.
To see how well it works, try superimposing your pitch estimates on a spectrogram of the recording.
Exercise 3 If you did the exercises in the previous chapter, you downloaded the historical price of BitCoins and estimated the power spectrum of the price changes. Using the same data, compute the autocorrelation of BitCoin prices. Does the autocorrelation function drop off quickly? Is there evidence of periodic behavior?
Exercise 4 In the repository for this book you will find a Jupyter notebook called saxophone.ipynb that explores autocorrelation, pitch perception, and a phenomenon called the missing fundamental. Read through this notebook and run the examples. Try selecting a different segment of the recording and running the examples again.
Vi Hart has an excellent video called “What is up with Noises? (The Science and Mathematics of Sound, Frequency, and Pitch)”; it demonstrates the missing fundamental phenomenon and explains how pitch perception works (at least, to the degree that we know). Watch it at https://www.youtube.com/watch?v=i_0DXxNeaQ0.
感謝翻譯,很有幫助,但發現5.1 Pearson’s correlation cofficient的公式有錯誤,分子XY兩項應該是相乘(Xi-Ux)'*'(Yi-Uy)。
回覆刪除改好了,感謝
刪除