[超譯]ThinkDSP 第三章

第三章 非週期訊號 | Non-periodic signals

目前為止我們遇到的訊號都是週期性的，這表示它們會一直一直重複。這也表示它們的頻率成份不會隨著時間改變。在這章，我們要考慮非週期訊號，它的頻率成份會隨時間改變。換句話說，幾乎所有的聲音訊號都會隨時間改變。
這章也介紹 spectrograms，這是一個視覺化非週期訊號的常用方法。
這章的程式碼在 chap03.ipynb，它的位置請看0.2節。你也可以在這看到它 http://tinyurl.com/thinkdsp03

3.1 線性唧頻 | Linear chirp

---

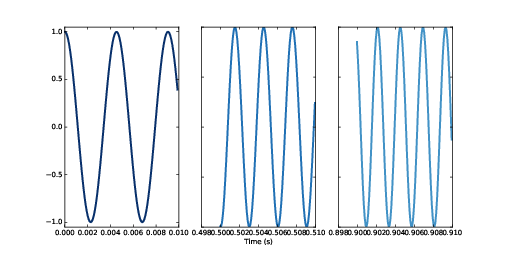
圖3.1：chirp 的波形，前段、中段 與尾段

---

我們先來看一個叫 chirp 的波，這訊號有著會變動的頻率。thinkdsp 提供一個繼承自 Signal 的 Chirp 類別，它是一個會隨著線性變化的頻率擺動的正弦波。
這裡介紹一個範例，頻率從 200 Hz 到 880 Hz 擺動，這會是兩個 8 度的音程從 A3 到 A5：

signal = thinkdsp.Chirp(start=220, end=880)
wave = signal.make_wave()

圖3.1 顯示這個波的片段，接近開頭，中間，結尾。可以清楚看到頻率是增加的。
在往下走之前，看一下 Chirp 是如何實作的：

class Chirp(Signal):

    def __init__(self, start=440, end=880, amp=1.0):
        self.start = start
        self.end = end
        self.amp = amp

start、end 是啟始與結束的頻率，單位 Hz。amp 是振幅。
接下來是訊號的評估函式：

def evaluate(self, ts):
    freqs = np.linspace(self.start, self.end, len(ts)-1)
    return self._evaluate(ts, freqs)

ts 是時間點的序列，代表要被評估的時間點，要保持這個函式簡單，我假設它是等間隔的。
如果 ts 的長度是 n，那這個序列的時間的間隔的數目就是 n-1。要計算每個間隔的頻率，我使用 np.linspace，它會回傳 numpy array，它有 n-1 個值，從 start 線性分佈到 end。
_evaluate 是個私有方法，它把剩下的數學做完：

def _evaluate(self, ts, freqs):
    dts = np.diff(ts)
    dphis = PI2 * freqs * dts
    phases = np.cumsum(dphis)
    phases = np.insert(phases, 0, 0)
    ys = self.amp * np.cos(phases)
    return ys

np.diff 會計算 ts 裡相鄰兩個元素的差，回傳每個間隔的長度，單位是秒。如果 ts 是等間距，dts 就會全部一樣。
下一步是搞懂每個間隔之間相位變化。在第1.7節，那時的頻率是常數，相位 $\varphi$ 是隨時間線性增加：
$$\varphi = 2 \pi f t$$
當頻率變成了時間的函式，相位的變化在一個很短的時間間隔Δ t會是：
$$\Delta \varphi = 2 \pi f(t) \Delta t$$
在 python 因為 freqs 包含f(t)、dts 包含時間間隔，我們可以寫成：

dphis = PI2 * freqs * dts

現在，因為 dphis 包含相位變化，我們可以利用把變化相加來得到整個相位：

phases = np.cumsum(dphis)
phases = np.insert(phases, 0, 0)

np.cumsum 計算的是累計的和，這幾乎是我們要的，只差它不是從 0 開始，所以我們用 np.insert 加一個 0 在前頭。
結果得到的是一個 numpy array，它的第 i 個元素就是包含前 i 個 dphis 的元素們的和，也就是在第 i 個時間間隔的尾巴的相位。最後，就是用 np.cos 計算波的振幅。(相位的單位是弧度)
如果你會一點微積分，會注意到 Δ t 在足夠小的時候會得到
$$\mathrm d \varphi = 2 π f(t) \mathrm d t$$
兩邊同除 d t 會得到
$$\frac{\mathrm d \varphi} {\mathrm d t} = 2 π f(t)$$
換言之，頻率是相位的導數。反過來說，相位是頻率的積分結果。當我們使用 cumsum 從頻率得到相位，我們做了個近似積分的動作。

3.2 指數唧頻 | Exponential chirp

當你聽線性唧頻的時候，你也許有注意到音高一開始升高很快，後來則趨緩。這個唧頻跨了兩個八度，但它只用了 2/3 秒就爬到第一個八度，然後用兩倍的時間爬到第二個八度。
原因是，我們感知音高是依據它的頻率的對數。我們聽到兩個音符的音程是依據它們頻率的比例，而不是頻率相減的差。音程是音樂術語，代表兩個音高的差距。
舉例來說，一個八度的音程差，是兩個音高的頻率比例為 2。所以音程從 220 Hz 到 440 Hz 是一個八度，從 440 HZ 到 880 Hz 也是一個八度。頻率相減的差變大了，但是比例都是一樣為 2。
所以，如果頻率線性升高，就像在線性唧頻，感知到的音高增加是對數增加。
如果要感覺上是線性的音高升高，那頻率增加就要指數增加，這樣子的訊號就叫指數唧頻。
接下來就是它的程式碼：

class ExpoChirp(Chirp):

    def evaluate(self, ts):
        start, end = np.log10(self.start), np.log10(self.end)
        freqs = np.logspace(start, end, len(ts)-1)
        return self._evaluate(ts, freqs)

現在不用 np.linspace 而是改用 np.logspace，這樣會讓頻率在取對數後是等寬，也就是它們是指數增加。
就這樣，剩下就跟原來的 Chirp 一樣，使用方法是：

signal = thinkdsp.ExpoChirp(start=220, end=880)
wave = signal.make_wave(duration=1)

你可以聽聽 chap03.ipynb 裡的這些範例，比較一下線性與指數唧頻。

3.3 唧頻的頻譜 | Spectrum of a chirp

---

圖3.2：一秒鐘一個八度的 chirp 的頻譜

---

當你計算唧頻的頻譜時，你覺得會發生什麼事？這有個例子是建立一秒鐘，一個八度的唧頻以及它的頻譜：

signal = thinkdsp.Chirp(start=220, end=440)
wave = signal.make_wave(duration=1)
spectrum = wave.make_spectrum()

圖3.2 顯示了這個結果。這頻譜在 220 到 440 Hz 之間有很多成份，它變化的樣子就像是魔戒中索侖的眼(http://en.wikipedia.org/wiki/Sauron)
頻譜在 220 到 440 HZ 之間約是平的，這說明這區間中，每個頻率佔用的時間差不多一樣。根據這個觀察，你應該可以猜到指數唧頻長什麼樣子。
頻譜約略給了訊號結構的樣子，但卻沒有顯示頻率與時間的關係，我們無法在這頻譜圖中看到頻率是否隨時間上升或下降或改變。

3.4 時頻圖 | Spectrogram

---

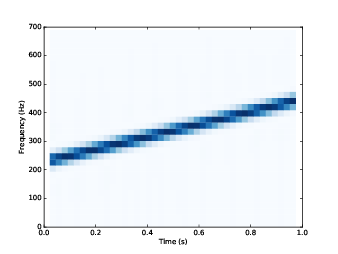
圖3.3：一秒鐘八度的唧頻的 spectrogram

---

要得到頻率與時間的關係，我們可以把唧頻切成一小段一小段的來畫頻譜。這結果就是所謂的 short-time Fourier Transform(STFT)。
有幾個方法可以把 STFT 視覺化，但最常用的是 spectrogram，它把時間畫在 x 軸，頻率畫在 y 軸。每個直行畫出一小段的頻譜，用顏色或灰階來代表振幅。
這個唧頻的 spectrogram 的計算是這樣：

signal = thinkdsp.Chirp(start=220, end=440)
wave = signal.make_wave(duration=1, framerate=11025)

Wave 提供 make_spectrogram 方法產生 Spectrogram 物件：

spectrogram = wave.make_spectrogram(seg_length=512)
spectrogram.plot(high=700)

seq_length 是每個小段要取多少數目的點。我選 512 是因為 FFT 在取樣數在 2 的次方倍時最有效率。
圖3.3 顯示這個結果，x 軸是時間從 0 到 1 秒。y 軸是頻率從 0 到 700 Hz。我把 spectrogram 上半部切掉，整個範圍會到 5512.5 Hz，是 framerate 的一半。
spectrogram 很清楚顯示頻率隨時間線性增加，然而，每個尖峰會暈開兩到三個小格，這反映出 spectrogram 的解析度的極限。

3.5 Gabor 極限 | The Gabor limit

Spectrogram 的時間解析度是每個片段的持續時間，它對應到 spectrogram 中每個小格的寬度。每個小段是 512 個 frame。因為每秒有 11025 個 frame，所以每個片段是 0.046 秒。
頻率解析度是頻譜中元素之間的頻率範圍，它對應到每個小格的高度。因為每個片段是 512 個 frame，我們在 0 到 5512.5 Hz 之間最多可切到 256 個頻率成份，每個成份的範圍是 21.6 Hz。
更一般地來說，如果 n 是片段的長度，則頻譜包含了 n/2 個成份。如果 r 是 framerate，那在頻譜中最大的頻率是 r/2。所以時間解析度是 n/r，頻率解析度是
$$\frac{r/2}{n/2} = r/n$$
理想上，我們想讓時間解析度小，這樣我們可以看到頻率有比較快速的變化。我們讓頻率解析度小，這樣我們可以看到比較小的頻率變化。但我們沒辦法兩個好處都要。因為時間解析度是 n/r，它正好是頻率解析度 r/n 的倒數，所以一個變小，另一個就變大。
例如，你讓片段的長度變兩倍長，可讓頻率解析度縮小成一半(這是好事)，但會讓時間解析度變大為兩倍(這是壞事)。就算增加 framerate 也沒有幫助，你得到更多的取樣點，頻率的範圍也同時增加。
這個魚與熊掌的問題叫做 Gabor 極限。這是時間-頻率分析的基本限制。

3.6 洩漏 | leakage

---

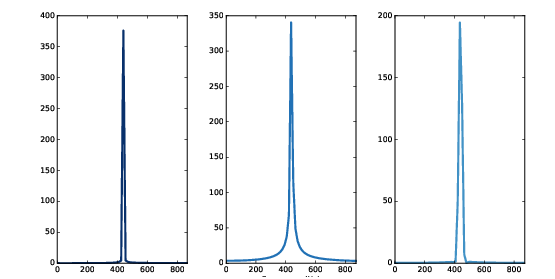
圖3.4：週期正弦曲線的頻譜(左圖)，非週期的片段(中圖)，window 過的非週期片段(右圖)

---

為了要解釋 make_spectrogram 的運作，我必須先解釋 windowing。而為了要解釋 windowing，我必須先介紹它要解決的問題。那問題叫做 leakage。
離散傅立葉轉換(DFT)是我們用來計算頻譜的，它認為波是週期的，也就是它假設所操作的片段是一個具完整週期、來自隨著時間無限重覆的訊號。在實務上，這假設通常是錯的，所以就造成問題。
一個常見的問題是片段的開頭與結尾是不連續的。因為 DFT 假設訊號是週期的，它隱含的一個意思是把片段的尾巴接到片段的頭會形成一個迴圈。如果，結尾沒有很平滑的接到開頭，那不連續的情況就會產生多出來的頻率成份，那本來不在訊號裡的。
來個例子，我們來個正弦曲線的訊號，頻率只有一個 440 Hz。

signal = thinkdsp.SinSignal(freq=440)

如果我們選一個小段的長度剛好是週期的整數倍，片段的結尾與開頭平滑地接在一起，DFT 的處理結果會很好。

duration = signal.period * 30
wave = signal.make_wave(duration)
spectrum = wave.make_spectrum()

圖3.4 左圖，如預期只有一個尖峰在 440 Hz。
但，如果持續時間不是週期的整數倍，壞事就發生了。當 duration = signal.period * 30.25，訊號開頭為 0，結尾為 1。
圖3.4 中間，440 Hz 有個尖峰，但有許多成份散在 240 到 640 Hz。這散佈叫做頻譜洩漏(spectral leakage)，因為在基頻的一些能量洩漏到別的頻率去。
在這個例子中，leakage 是因為我們把不連續的小段當成週期性的，然後用 DFT 處理而發生。

3.7 窗 | Windowing

---

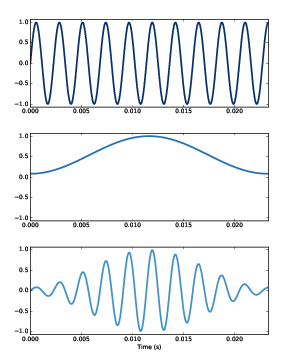
圖3.5：正弦曲線的小段(上圖)、Hamming window (中圖)、小段與 window 相乘的結果 (下圖)

---

把開頭與結尾不連續的地方想辦法平滑地接起來，我們可以減少 leakage，其中一個方法叫做 windowing。
一個 “window” 函數是被設計出來的，目的是為了要把非週期的片段，變成長得像是週期的樣子。圖3.5 的上面，顯示一個片段，他的開頭與結尾沒有平滑地接在一起。
圖3.5 的中間，顯示一個 Hamming window，這是最常用的 window 函數之一。沒有任何window函數是完美的，有些是為了不同的目的而優化的。Hamming 是個夠好，適合許多場合的函數。
圖3.5 下面，顯示 window 函數與原來訊號相乘的結果。在 window 函數的值接近一的地方，訊號沒有改變。在 window 函數的值接近 0 的地方，訊號則被抑制。因為 window 的兩邊是壓扁的，所以相乘出來的訊號，兩邊的值接近 0，所以可以平滑地接在一起。
圖 3.4 右邊的圖，是這個 window 過的訊號的頻譜。windowing 的確減低了 leakage，但沒辦法全部消除。
接下來看程式碼的樣子。Wave 類別提供 window 方法，它可以應用 Hamming window：

#class Wave:
    def window(self, window):
        self.ys *= window

numpy 提供 hamming 函數，計算出給定長度的 Hamming window 的值：

window = np.hamming(len(wave))
wave.window(window)

numpy 提供了其他的 window 函數，包含 bartlett、blackman、hanning、kaiser。這章的結尾的習題之一，會要求你試試其他的 window 函數。

3.8 實作時頻圖 | Implementing spectrograms

---

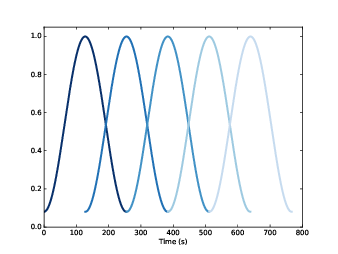
圖3.6：重疊的 Hamming window

---

現在我們了解 windowing，接下來就可以了解 spectrogram 的實作了。接下來是 Wave 物件用來計算 spectrogram 的程式碼：

#class Wave:
    def make_spectrogram(self, seg_length):
        window = np.hamming(seg_length)
        i, j = 0, seg_length
        step = seg_length / 2

        spec_map = {}

        while j < len(self.ys):
            segment = self.slice(i, j)
            segment.window(window)

            t = (segment.start + segment.end) / 2
            spec_map[t] = segment.make_spectrum()

            i += step
            j += step

        return Spectrogram(spec_map, seg_length)

這是這本書裡最長的函式，所以，你可以搞定的話，其他的也都可以。
self，代表 Wave 物件(實體)自己。seg_length 是每個片段的取樣的數目。
window 是 Hamming window，長度與片段的長度一樣。
i 與 j 是切段的指標(index)，用來從 wave 物件取出片段。step 是每個片段之間的位移。因為 step 是 seg_length 的一半，所以片段會與另一個片段重疊一半。圖3.6 顯示這個重疊的 window 的樣子。
spec_map 是一個字典，把時間戳記與頻譜對應起來。
在 while 回圈內，我們從 wave 選一個片段，並且乘上 window。然後產生這段的頻譜 spectrum 物件，然後加到 spec_map 去。每個片段的時間，我們選中間值來代表。
然後，我們移動 i 與 j，再做一次，只要 j 沒超過 wave 的尾巴，就一直重覆。
最後，這個方法回傳一個 spectrogram 物件。Spectrogram 的定義：

class Spectrogram(object):

    def __init__(self, spec_map, seg_length):
        self.spec_map = spec_map
        self.seg_length = seg_length

跟很多 init 一樣，這個也只是把參數存在屬性值。
Spectrogram 提供 plot 方法，這會產生 pseudocolor 圖，它的 x 軸是時間，y 軸是頻率。
這就是 Spectrogram 的實作方式。

3.9 練習

Solutions to these exercises are in chap03soln.ipynb.
Exercise 1 Run and listen to the examples in chap03.ipynb, which is in the repository for this book, and also available at http://tinyurl.com/thinkdsp03.
In the leakage example, try replacing the Hamming window with one of the other windows provided by NumPy, and see what effect they have on leakage. See http://docs.scipy.org/doc/numpy/reference/routines.window.html
Exercise 2 Write a class called SawtoothChirp that extends Chirp and overrides evaluate to generate a sawtooth waveform with frequency that increases (or decreases) linearly.
Hint: combine the evaluate functions from Chirp and SawtoothSignal.
Draw a sketch of what you think the spectrogram of this signal looks like, and then plot it. The effect of aliasing should be visually apparent, and if you listen carefully, you can hear it.
Exercise 3 Make a sawtooth chirp that sweeps from 2500 to 3000 Hz, then use it to make a wave with duration 1 s and frame rate 20 kHz. Draw a sketch of what you think the spectrum will look like. Then plot the spectrum and see if you got it right.
Exercise 4 In musical terminology, a “glissando” is a note that slides from one pitch to another, so it is similar to a chirp.
Find or make a recording of a glissando and plot a spectrogram of the first few seconds. One suggestion: George Gershwin’s Rhapsody in Blue starts with a famous clarinet glissando, which you can download from http://archive.org/details/rhapblue11924.
Exercise 5 A trombone player can play a glissando by extending the trombone slide while blowing continuously. As the slide extends, the total length of the tube gets longer, and the resulting pitch is inversely proportional to length.
Assuming that the player moves the slide at a constant speed, how does frequency vary with time?
Write a class called TromboneGliss that extends Chirp and provides evaluate. Make a wave that simulates a trombone glissando from C3 up to F3 and back down to C3. C3 is 262 Hz; F3 is 349 Hz.
Plot a spectrogram of the resulting wave. Is a trombone glissando more like a linear or exponential chirp?
Exercise 6 Make or find a recording of a series of vowel sounds and look at the spectrogram. Can you identify different vowels?

---

註1：方法名字若是用 _ (底線) 開頭的，就表示它是私有的，不是 API 的一部份，不應該在類別定義的外面使用。