[超譯]ThinkDSP 第一章

第一章 聲音與訊號 | Sounds and Signals

訊號表示一個數值，那數值隨著時間或空間改變，也可以隨時間與空間改變。這定義相當抽象，所以，我們從一個實際例子開始，聲音是空氣壓力的變化。一個聲音訊號就是表示隨著時間的空氣壓力的變化。
麥克風是一個裝置，量測這些變化且產生電子訊號來表示聲音。喇叭是一個裝置，會依電子訊號產生聲音。麥克風與喇叭，都叫做傳感器 transducer，因為它們能夠傳遞或是轉換訊號，從一個型式到另一個型式。
這本書講的是訊號處理，包含了合成(synthesizing)、轉換(transforming)、分析(analyzing)訊號的處理方式。我會著重在聲音，但這些方法同樣可以用在電子訊號、機械振動，與其他領域的訊號。
而且，不只是隨時間變化的訊號，這些方法也可以用在隨空間變化的訊號，像是沿著登山步道的高度。而且，也可以用於多維度的訊號，你可以把影像想做是二維隨空間變化的訊號。或著如電影，你可以把它想做是二維隨時間與空間變化的訊號。
那我們從一維的訊號「聲音」開始吧。
這章的程式碼在 chap01.ipynb，(若不知道在哪兒找它，請看 0.2 那一節)也可以在這裡找到 http://tinyurl.com/thinkdsp01 。

1.1 週期訊號 | Periodic signals

---

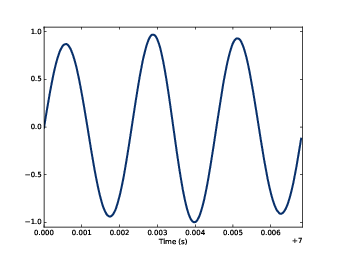
圖1.1：鐘聲的錄音片段

---

我們一開始介紹週期訊號，它是會不斷重覆的訊號，而且固定時間間隔就重覆一次。例如，如果你敲鐘，它會振動然後產生聲音，如果你記錄下這個聲音然後畫出它的訊號，它會看起來像是圖1.1。
這個訊號類似於正弦曲線 sinusoid，這意味著他與三角函數裡的正弦函數 sine 有相同形狀。
你可以看到這訊號是週期的，我選擇一個時間區期可以放下三個完整的週期 period，也可以說成循環 cycle。每個週期的時間約為 2.3 ms。
一個訊號的頻率，就是每秒有幾個週期的訊號，它剛好是週期的倒數。頻率的單位是 Hertz，簡寫 Hz。
上面的例子，訊號的頻率是 439 Hz，略低於 440 Hz。440 Hz 是交響樂用來調音的頻率，音符名是 A，或精確地說是 A4。如果你不熟這些音樂符號，只要知道 A4 是比中央 C 高一點的那個 A，A5 比 A4 還要高八度音，其他就去看 wiki： http://en.wikipedia.org/wiki/Scientific_pitch_notation

---

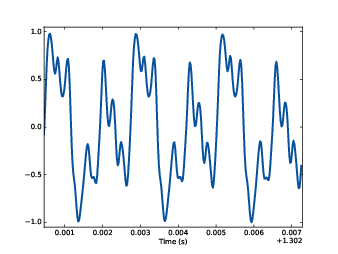
圖1.2：小提琴的錄音片段

---

音叉產生的訊號是正弦曲線，因為它的振動是簡諧運動。多數的樂器產生週期訊號，但訊號形狀不是正弦曲線。例如圖 1.2，它是從波契里尼的 E 大調 弦樂五重奏第5號，第三樂章的小提琴錄下來的。
我們一樣可以看到這是週期函數，但是訊號形狀比較複雜。週期訊號的形狀，我們叫它做波形。大多樂器的波形都比正弦曲線複雜，波形會決定樂器的音色，這是我們對聲音品質的認知。人們通常會認為複雜波形的聲音比正弦形狀的聲音較豐富、較有趣。

1.2 頻譜分解 | Spectral decomposition

---

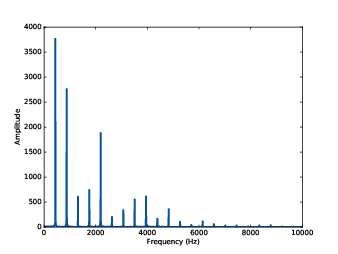
圖1.3：小提琴的錄音片段的頻譜

---

在這本書最重要的主題就是頻譜分解 spectral decomposition。這概念是，任何訊號都可以用不同頻率的正弦函數相加來表示。
在這本書最重要的數學概念是離散傅立葉轉換 discrete Fourier transform，簡寫 DFT。它把訊號以頻譜的方法表現，頻譜就是一組正弦函數組成，把它加起來就會得到原來的訊號。
然後，這本書最重要的演算法就是快速傅立葉轉換 Fast Fourier transform，簡寫 FFT，這是一個有效率算出 DFT 的方法。
例如，圖1.3 就是 圖1.2 的小提琴的頻譜。x 軸是訊號的頻率範圍，y 軸是每個成份頻率的強度或說是振幅。
最低的成份頻率叫做基頻，這個訊號的基頻接近 440 Hz。(實際上有低了一點點)
這個訊號的基頻有最大的振幅，所以我們也說那是它的主頻。通常一個聲音的音高的頻率，我們會以它的基頻來決定而不是它的主頻。
在頻譜裡的其他尖尖的，在 880，1320，1760，及 2200，這些都是基頻的整數倍的頻率。這些成份都叫做諧波 harmonic，因為在音樂上這些音會與基音聽起來和諧。

• 880 是 A5 的頻率，比基音高 8 度。高一個八度在頻率上是原音的兩倍。
• 1320 接近 E6，比 A5 高五度。如果不熟悉音程的人，請參閱 https://en.wikipedia.org/wiki/Interval_(music)
• 1760 是 A6，比基音高兩個 8 度。
• 2200 接近 C#7，比 A6 高三度。

這些諧波組成一個 A 和弦，雖然不在同一個 8 度裡。它們有些是近似音，因為這些音符被西方音樂的平均律調整過了。(請參閱 http://en.wikipedia.org/wiki/Equal_temperament) [譯註：所以是音符的問題，不是音高的問題，不要太講究了。]
有了這些諧波與振幅，你可以把這些正弦曲線加起來以重建這個訊號。接下來看如何辦到。

1.3 訊號(類別) | Signals

我寫了個 python 的模組，叫做 thinkdsp.py，裡面包含類別與函式，可用來處理訊號與頻譜(註1)。(不知道去哪兒找請看0.2)
要表示一個訊號，thinkdsp 提供一個類別叫做 Signal，這是許多訊號類型的父類別，像 Sinusoid 就是它的子類別。Sinusoid 可以表示 sine 與 cosine 的訊號。
thinkdsp 提供函式來製造 sine 與 cosine 的訊號：

cos_sig = thinkdsp.CosSignal(freq=440, amp=1.0, offset=0)
sin_sig = thinkdsp.SinSignal(freq=880, amp=0.5, offset=0)

freq 是頻率，單位 Hz。amp 是振幅，它沒有指定單位，1.0 是指我們可以錄到或播放的最大振幅。
offset 是指相位移，單位是 radians。相位移是決定在週期中訊號的啟始點。例如，sine 訊號若是 offset=0，那它會從 sin0 開始，值是 0。若是 offset=pi/2，那它會從 sin(pi/2) 開始，值是 1。
訊號有 __add__ 的方法，所以你可以用 + 操作來相「加」。

mix = sin_sig + cos_sig

這結果就是一個 SumSignal，它是用來表示兩個或多個相加的訊號。
一個 Signal 物件基本上是數學函式的 python 表達方式，多數訊號的時間區域是定義成任何時間，也就是從負無限大到正無限大。
對一個 Signal 物件，要對它做更多應用就要評估(evaluate)它，在這裡，評估(evaluate)的意思是，取得時間的序列點ts，計算對應的訊號值 ys。我用 numpy 的 array 存放 ts 與 ys。然後封裝在一個叫做 Wave 的物件。
一個 Wave 物件用一序列的時間點，以及時間點對應的值來表示一個訊號。每一個時間點，叫做一個 frame(這名詞從電影及影片借來的)。每個值叫做 sample，雖然有時候 frame 與 sample 兩個字會交叉著用。
Signal 提供 make_wave 方法，可以傳回一個新的 Wave 物件。

wave = mix.make_wave(duration=0.5, start=0, framerate=11025)

duration 是指 Wave 的長度，單位是秒。start 是指開始時間，單位也是秒。framerate 是指每秒幾個 frame，必須是正整數，也就是每秒幾個 sample 的意思。
每秒 11025 frames 這個 framerate，是音樂檔中幾個常用的值之一，像是 Waveform Audio File (WAV) 及 mp3。
這個範例評估了訊號從 t=0 到 t=0.5，在 5513 個等間隔的 frame(因為 11025 的一半是 5513)。兩個 frame 之間的時間，或說是 timestep 是 1/11025 秒，也就是 91 µs。
Wave 物件提供了 plot 方法，它使用 pyplot 來畫圖。你可以像這樣畫：

wave.plot()
pyplot.show()

pyplot 是 matplotlib 的一部份，在許多 python 包有，或者你可以自己安裝。

---

圖1.4：兩個正弦曲線的組合的片段

---

freq=440，在 0.5 秒之內，會有 220 個週期，所以直接畫會看到一團顏色。要放大到只看到幾個週期的話，我們可以用 segment，它會複製一小段 Wave 然後回傳成一個新的 wave。

period = mix.period
segment = wave.segment(start=0, duration=period*3)

period 是 Signal 的性質，會回傳它的週期，單位是秒。
start 與 duration 單位也是秒，這範例複製 mix 的前三個週期。
如果我們把 segment 畫出來，就是圖1.4，這個訊號包含兩個成份頻率，所以它比音叉的波形複雜一點，但又沒像小提琴那樣複雜。

1.4 讀寫波形(檔) | Reading and writing Waves

thinkdsp 提供 read_wave 方法，這會讀取一個 WAV 檔，傳回一個 Wave 物件。

violin_wave = thinkdsp.read_wave('input.wav')

同時， Wave 也提供 write 方法，可以寫成一個 WAV 檔：

wave.write(filename='output.wav')

你可以用任何多媒體播放器(可聽 WAV 檔)聽 Wave 的聲音。在 UNIX 系統，我用 aplay，它在很多 linux 系統裡都有。
thinkdsp 也提供 play_wave 方法，它會用 subprocess 來呼叫多媒體播放器：

thinkdsp.play_wave(filename='output.wav', player='aplay')

它內定用 aplay，但你也可以指名用其他的 player。

1.5 頻譜 | Spectrums

Wave 物件提供 make_spectrum 方法，可以傳回 Spectrum 物件

spectrum = wave.make_spectrum()

Spectrum 提供 plot 方法，可以畫出圖：

spectrum.plot()
thinkplot.show()

thinkplot 是我寫的一個模組，把 pyplot 裡面一些函式包裝起來。(要找到它可以看 0.2章)
Spectrum 提供三個方法可以修改頻譜：

• low_pass，提供低通濾波器 low pass filter，這意思就是高於某個頻率的成份會被抑制，也就是頻率高於某個值的成份，就依照某個比例把振幅縮小。
• high_pass，提供提供高通濾波器 high pass filter，抑制某個頻率的以下的成份。
• band_stop，帶阻濾波器，在兩個頻率之間的成份要被抑制。

以下舉例，把高於 600 的頻率抑制 99%：

spectrum.low_pass(cutoff=600, factor=0.01)

low pass filter 會移除明亮、高頻率的聲音，所以產生出悶悶的、暗暗的聲音。要聽這聲音像什麼，可以把 spectrum 轉回 Wave，然後播放它：

wave = spectrum.make_wave()
wave.play('temp.wav')

play 這個方法會把 wave 寫回成檔案，然後播放它。如果你用 Jupyter notebook，可以使用 make_audio，這會建立一個 Audio widget，它可以播放聲音。

1.6 波形物件 | Wave objects

---

圖1.5：thinkdsp 裡的類別的關係

---

thinkdsp.py 裡面沒有什麼複雜的東西，多數函式只是提供一個輕巧的包裝，讓 numpy 與 scipy 比較方便用。
thinkdsp 裡面主要的類別是 Signal, Wave, Spectrum。給定一個 Signal，就可以製造一個 Wave。給定一個 Wave，就可以製造一個 Spectrum。反過來從 Spectrum 製造一個 Wave 也行。其中關係可以看圖1.5。
Wave 物件有三個性質，ys 是一個 numpy 的 array，裡面的值是 signal 的值；ts 也是個 array，裡面的值是訊號值評估(evaluate)的時間或是取樣(sample)的時間；framerate 是每單位時間取樣的次數。時間的單位通常是秒，但不一定非是秒不可。我有個例子是以天為單位。
Wave 也提供三個唯讀的性質，start, end, duration，如果你改變 ts，這些性質也會跟著變。
要改變一個 wave，你可以直接去動 ts, ys。例如：

wave.ys *= 2
wave.ts += 1

第一行會產生的影響是訊號放大兩倍，聲音大聲。第二行是讓 wave 在時間上移動，讓它晚一秒鐘開始。
Wave 提供更一般化的方法來做這事情，例如要達到同樣效果，可以這樣寫

wave.scale(2)
wave.shift(1)

你可以查看 thinkdsp 的文件，看有哪些東西：http://greenteapress.com/thinkdsp.html

1.7 訊號物件 | Signal objects

Signal 是所有訊號類別的父類別，提供一般化的函式給所有子類別使用。像是 make_wave。子類別繼承這些方法並提供 evaluate(評估) 方法，這會依給定的時間序列評估(計算)訊號的值。
例如，Sinusoid 物件(正弦曲線物件)是 Signal 物件的子物件，它是這樣定義的：

class Sinusoid(Signal):
    def __init__(self, freq=440, amp=1.0, offset=0, func=np.sin):
        Signal.__init__(self)
        self.freq = freq
        self.amp = amp
        self.offset = offset
        self.func = func

__init__ 的參數是

• freq：頻率，每秒幾個循環，單位 Hz。
• amp：振幅，這個單位沒有固定，通常選擇是 1.0 是對應到麥克風的輸入值的最大值，或是喇叭的輸入值的最大值。
• offset：指示在一個週期中，訊號要從何處開始。單位是 radian (弧度)。理由之後會說明。
• func：是指 python 的函式，可用來產生訊號的，是要被某些特定時間點評估出訊號值。通常會選的是 np.sin 或 np.cos，如此得到 sine 或 cosine 的訊號。

如同許多的 init 方法，這一個也只是把參數放進物件內後供以後使用。
Signal 物件提供 make_wave 方法，它長成這樣：

def make_wave(self, duration=1, start=0, framerate=11025):
    n = round(duration * framerate)
    ts = start + np.arange(n) / framerate
    ys = self.evaluate(ts)
    return Wave(ys, ts, framerate=framerate)

start 與 duration 是開始時間與持續時間，單位是秒，framterate 是每秒幾幀(frame)，或說是每秒幾個取樣。
n 是取樣的數目，ts 是 numpy 的 array，裝的是取樣時間。
為了要計算 ys，make_wave 呼叫 evaluate，它是由 Sinusoid 提供：

def evaluate(self, ts):
    phases = PI2 * self.freq * ts + self.offset
    ys = self.amp * self.func(phases)
    return ys

讓我們一步一步來看：

1. self.freq，是每秒幾個循環，每個 ts 裡的元素是時間，單位是秒，所以它們相乘所得到的是從開始時間到當時有幾個循環。
2. PI2 是一個常數，就是 2π 的意思。乘上 PI2，會讓循環(cycle)變成相位(phase)。你可以把相位想成是從開始時間有幾個循環，但是單位是弧度(radian)，每個循環是 2π 的弧度。
3. self.offset 是 t=0 時的相位，它可以在時間上，把訊號向左移或向右移。
4. 如果，self.func 是 np.sin 或 np.cos，那產生的值會是 -1 到 1 之間。
5. 把產生出來的值，乘上 self.amp，會得到值是在 -self.amp 到 +self.amp 之間。

在數學的表示上，evaluate 會長成這樣：
$$y = A cos(2 \pi f t + \phi_0)$$
A 是 amplitude，也就是振幅，f 是頻率，t 是時間，相位的位移。這看起來跟我寫一大堆程式碼的效果一樣，但接下來會看到，這些程式碼可以提供一個架構讓所有的訊號都可用，而不只是正弦曲線而已。

1.8 練習

在你開始以下的練習前，你應該先下載這本書要用的程式碼，請依0.2節的指示進行。
這些習題的解答在 chap01soln.ipynb。
[譯註，習題不翻譯，請大家練習看英文，從題目與解答中可以對照出自己有沒有瞭解題意。]
Exercise 1 If you have Jupyter, load chap01.ipynb, read through it, and run the examples. You can also view this notebook at http://tinyurl.com/thinkdsp01.
Exercise 2 Go to http://freesound.org and download a sound sample that includes music, speech, or other sounds that have a well-defined pitch. Select a roughly half-second segment where the pitch is constant. Compute and plot the spectrum of the segment you selected. What connection can you make between the timbre of the sound and the harmonic structure you see in the spectrum?
Use high_pass, low_pass, and band_stop to filter out some of the harmonics. Then convert the spectrum back to a wave and listen to it. How does the sound relate to the changes you made in the spectrum?
Exercise 3 Synthesize a compound signal by creating SinSignal and CosSignal objects and adding them up. Evaluate the signal to get a Wave, and listen to it. Compute its Spectrum and plot it. What happens if you add frequency components that are not multiples of the fundamental?
Exercise 4 Write a function called stretch that takes a Wave and a stretch factor and speeds up or slows down the wave by modifying ts and framerate. Hint: it should only take two lines of code.

---

註1：spectrum 常常寫做 spectra，但我偏好使用標準的複數名詞。如果你習慣用 spectra，我希望我的選擇不會太奇怪。